Trong các ngôn ngữ lập trình, khả năng lưu trữ của kiểu số thường có 1 giới hạn. Ví dụ kiểu dữ liệu int của ngôn ngữ C++ thường giới hạn ở mức –2.147.483.648 đến 2.147.483.647.
Có những bài toán thực tế cần thao tác với những số vượt quá giới hạn này. Do đó cần phải có những phương pháp để giải quyết như:
- Sử dụng những thư viện hỗ trợ thêm.
- Tự xây dựng các kiểu dữ liệu này và cung cấp các phương thức lưu trữ và thao tác.
Phép cộng hai số lớn
Lựa chọn kiểu dữ liệu
Với một số nguyên lớn có 20 độ dài 20 ký số, một biến thông thường không thể hiện được toàn bộ số lớn này. Vì vậy chọn cách dùng nhiều biến để biểu diễn từng chữ số, như vậy có thể sử dụng một mảng các ký số để biểu diễn cho một số lớn.
Một chữ số có giá trị từ 0 – 9 nên để tối ưu và đơn giản cho thao tác nhập mảng, có thể sử dụng mảng kiểu char[].
Hàm cộng hai số lớn có dạng:
char* addBigNumber(char* number1, char* number2);
Với hai chuỗi number1, number2 là hai số lớn cần tính toán.
Hiện thực phép toán
Có 2 trường hợp sau khi cộng hai số number1 và number2:
number1có chiều dài (số ký số) lớn hơn hoặc bằng sốnumber2.number2có chiều dài lớn hơn hoặc bằng sốnumber1.
Để tổng quát hóa hai trường hợp trên, cần so sánh chiều dài hai số number1 và number2, nếu số number2 có chiều dài lớn hơn số number1, thực hiện đảo giá trị hai pointer chứa địa chỉ mảng number1 và mảng number2. Từ đó, number1 luôn có chiều dài lớn hơn hoặc bằng number2.
Để đơn giản cho thao tác với chuỗi, sử dụng hàm strlen() trong thư viện string.h.
if (strlen(number1) < strlen(number2))
{
swapPointer(&number1, &number2);
}
Hàm swapPointer được định nghĩa như sau:
void swapPointer(char** a, char** b)
{
char* temp = *a;
*a = *b;
*b = temp;
}Khai báo một số biến cần thiết trong quá trình tính toán như sau:
number1Len,number2Lenlà chiều dài hai sốnumber1,number2.resultlà kết quảnumber1 + number2, chiều dài củaresultluôn bằng hoặc lớn hơn chiều dài sốnumber1một đơn vị tùy trường hợp nên khi cấp phát choresultcần thêm 1 byte và 1 byte nữa là dành cho ký tự rỗng cuối chuỗi là 2 byte.rememberlà biến chỉ trạng thái “nhớ” của phép tính khi cộng 2 chữ số, ban đầu làfalse.
size_t number1Len = strlen(number1), number2Len = strlen(number2); char* result = new char[number1len + 2]; bool remember = false;
Có hai công đoạn khi thực hiện cộng 2 số:
- Tính tổng các chữ số của cả
number1vànumber2(phần bên phải). - Tính tổng các chữ số của
number1với0(phần bên trái).
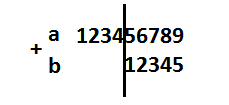
Như vậy cần hai vòng lặp để làm những việc này.
Bước 1
Số lần lặp của công đoạn này sẽ là number2_len
for (int i = 0; i < number2Len; i++)
{
//...
}
Cần tính tổng các chữ số từ phải qua trái, lấy giá trị các chữ số này bằng cách sử dụng number1[number1Len - i - 1] và number2[number2Len - i - 1].
Mỗi giá trị hiện tại đang được lưu trong mảng với kiểu char, để lấy được chính xác giá trị kiểu số của các chữ số này, trừ mỗi giá trị cho 48 ('0'). Ví dụ: ký tự '9' trong kiểu char có giá trị là 57, lấy 57 - 48 được 9.
Dùng một biến tạm để lưu tổng của 2 giá trị này:
int temp = number2[number2Len - i - 1] - '0' + number1[number1Len - i - 1] - '0';
Ví dụ: khi cộng 18 và 13, kết quả là 11 >= 10 nên chỉ lấy chữ số hàng đơn vị là 1, nhớ 1, tiếp theo, lấy 1 + 1 được 2, vì có nhớ nên ghi 3. Kết quả là 31.
Theo logic đó, tiếp xét giá trị biến remember, nếu là true thì cộng temp lên 1 đơn vị, nếu temp có giá trị >= 10, gán remember = true, ngược lại ta gán remember = false. Để lấy chữ số hàng đơn vị của temp, ta lấy temp chia phần dư cho 10.
if (remember) temp++; remember = temp > 9; temp = temp % 10;
Tổng các chữ số của number1 và number2 đã được tính với cách trên, gán giá trị này vào mảng result. Tương tự cách làm ở trên, để ghi được ký tự '9' vào mảng, cộng số 9 với 48 ('0').
*(result + number1Len - i) = temp + '0';
Vậy ta có code hoàn chỉnh cho vòng lặp vừa rồi như sau:
for (int i = 0; i < number2Len; i++)
{
int temp = *(b + number2Len - i - 1) - '0' + *(a + number1Len - i - 1) - '0';
if (remember)
temp++;
remember = temp > 9;
temp = temp % 10;
result[number1Len - i] = temp + '0';
}Với vòng lặp này, có thể cộng hai số lớn có chiều dài bằng nhau.
Bước 2
Tương tự các bước của công đoạn thứ nhất, số lần lặp của công đoạn này là: number1Len - number2Len.
Giai đoạn này lấy giá trị các ký số của number1 bằng cách sử dụng: number1[number1Len – number2Len – i - 1], từ đó có giá trị biến temp là:
int temp = number1[number1Len - number2Len - i – 1] - '0';
Tương tự giá trị result như sau:
result[number1Len - number2Len – i] = temp + '0';
Code hoàn chỉnh:
for (int i = 0; i < number1Len - number2Len; i++)
{
int temp = *(number1 + number1Len - number2Len - i - 1) - '0';
if (remember)
temp++;
remember = temp > 9;
temp = temp % 10;
result[number1Len - number2Len - i] = temp + '0';
}Để đánh dấu kết thúc chuỗi result, gán:
result[number1Len + 1] = '\0';
Ví dụ 1 + 9999, làm lần lượt các bước như trên, được result có 4 chữ số, nhưng đáp án là 10000 có 5 ký số. Để làm được việc này, xét giá trị biến remember, nếu là true: gán giá trị result[0] = '1', ngược lại, dịch tất cả các phần tử của mảng result sang bên trái một đơn vị.
if (remember)
{
result[0] = '1';
}
else
{
for (int i = 0; i <= number1Len; i++)
result[i] = result[i + 1];
}Cuối cùng, trả về result là kết quả của number1 + number2.
Kiểm thử với hàm main:
int main()
{
char* a = "12345678987654321", *b = "98765432123456789";
char* c = addBigNumber(a, b);
printf("%s", c);
delete[] c;
}Kết quả: 111111111111111110.
Code hoàn chỉnh cộng 2 số lớn
void swapPointer(char** a, char** b)
{
char* temp = *a;
*a = *b;
*b = temp;
}
char* addBigNumber(char* number1, char* number2)
{
if (strlen(number1) < strlen(number1))
{
swapPointer(&number1, &number2);
}
size_t number1Len = strlen(number1), number2Len = strlen(number2);
char* result = new char[number1Len + 2];
memset(result, '0', number1Len);
bool remember = false;
for (int i = 0; i < number2Len; i++)
{
int temp = number2[number2Len - i - 1] - '0' + number1[number1Len - i - 1] - '0';
if (remember)
temp++;
remember = temp > 9;
temp = temp % 10;
result[number1Len - i] = temp + '0';
}
for (int i = 0; i < number1Len - number2Len; i++)
{
int temp = number1[number1Len - number2Len - i - 1] - '0';
if (remember)
temp++;
remember = temp > 9;
temp = temp % 10;
result[number1Len - number2Len - i] = temp + '0';
}
result[number1Len + 1] = '\0';
if (remember)
{
result[0] = '1';
}
else
{
for (int i = 0; i <= number1Len; i++)
result[i] = result[i + 1];
}
return result;
}Phép trừ hai số lớn
Hàm trừ hai số lớn có dạng:
char* subBigNumber(char* number1, char* number2);
Với hai chuỗi number1, number2 là hai số lớn cần tính toán.
Hiện thực phép toán
Khi trừ hai số number1 và number2, phải biết số nào lớn hơn để thực hiện phép trừ. Ví dụ khi thực hiện phép toán 99 – 100. Xác định 100 lớn hơn 9 nên lấy 100 – 99 = 1, thêm dấu trừ và được kết quả -1.
Để cho thuận tiện kiểm tra number2 có lớn number1 hay không? Nếu có thì ta đảo hai pointer chứa địa chỉ hai mảng number1, number2 và thêm dấu trừ vào trước kết quả.
bool sign = false, remember = false;
if (strlen(number1) < strlen(number2))
{
sign = true;
swapPointer(&number1, &number2);
}
else if (strlen(number1) == strlen(number2))
{
for (int i = strlen(number1) - 1; i >= 0; i--)
{
if (*(number1 + i) < *(number2 + i))
{
swapPointer(&number1, &number2);
sign = true;
}
}
}Đoạn code trên kiểm tra độ dài 2 số, nếu bằng nhau sẽ tiếp tục so sánh từng chữ số từ phải qua trái để tìm ra số lớn hơn, sau đó đảo vị trí các pointer (nếu cần).
Khai báo và gán giá trị một số biến cần thiết trong quá trình tính toán như sau:
size_t number1Len = strlen(number1), number2Len = strlen(number2); char* result = new char[number1Len + 2]; memset(result, '0', number1Len + 2);
result được cấp phát thêm 2 bytes: một byte dành cho ký tự rỗng cuối chuỗi, một byte cho dấu trừ đầu chuỗi nếu kết quả là số âm.
Có hai công đoạn khi thực hiện trừ hai số:
- Tính hiệu các chữ số của
number1chonumber2(phần bên phải). - Tính hiệu các chữ số của
number1với0(phần bên trái).
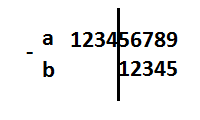
Như vậy cần hai vòng lặp để làm việc này.
Bước 1
Số lần lặp của công đoạn này là number2Len:
for (int i = 0; i < number2Len; i++)
{
//...
}Cần tính hiệu các ký số từ phải qua trái, vì phép trừ nên chỉ cần số chênh lệch giữa 2 số:
int temp = number1[number1Len - i - 1] - number2[number2Len – i - 1];
Theo như logic của phép trừ, khi một chữ số của number1 nhỏ hơn number2, khi trừ phải mượn 1 từ chữ số tiếp theo bên trái. Và kết quả phép trừ được cộng thêm 10, kết quả phép trừ tiếp theo sẽ giảm 1 đơn vị do mượn 1 từ phép trừ vừa rồi:
if (remember == true)
temp--;
if (temp < 0)
{
temp += 10;
remember = true;
}
else
remember = false;Gán kết quả vừa tính vào result:
result[number1Len – i] = temp + '0';
Code hoàn chỉnh cho vòng lặp vừa rồi như sau:
for (int i = 0; i < number2Len; i++)
{
int temp = number1[number1Len – i - 1] - number2[number2Len – i - 1];
if (remember == true)
temp--;
if (temp < 0)
{
temp += 10;
remember = true;
}
else
remember = false;
result[number1Len - i] = temp + '0';
}Bước 2
Số lần lặp của công đoạn này là: number1Len - number2Len.
Giai đoạn này chỉ cần lấy giá trị các ký số của number1 bằng cách sử dụng: number1[number1Len – number2Len – i], từ đó có giá trị biến temp là:
int temp = number1[number1Len - number2Len - i] - '0';
tương tự ta có giá trị result như sau:
result[number1Len - number2Len – i + 1] = temp + '0';
vậy ta có code hoàn chỉnh:
for (int i = 0; i < number1Len - number2Len; i++)
{
int temp = *(a + number1Len - number2Len – i - 1) - '0';
if (remember == true)
temp--;
if (temp < 0)
{
temp += 10;
remember = true;
}
else
remember = false;
result[number1Len - number2Len - i] = temp + '0';
}Ví dụ: 1000 – 999 với những gì đã làm ta được kết quả là 0001, xóa số 0 trước chuỗi và thêm dấu trừ (nếu có) vào đầu chuỗi dựa vào giá trị biến sign.
while (result[0] == '0')
{
if (result[1] != '0' && sign == true)
{
result[0] = '-';
result[number1Len + 1] = '\0';
break;
}
for (int i = 0; i < number1Len; i++)
{
result[i] = result[i + 1];
}
result[number1Len] = '\0';
}Cuối cùng, ta trả về result - kết quả của number1 - number2.
Test thử với hàm main:
int main()
{
char* a = "12345678987654321", *b = "98765432123456789";
char* c = subBigNumber(a, b);
printf("%s", c);
delete[] c;
}Ta được output: -6419753135802468 là chính xác.
Code hoàn chỉnh trừ 2 số lớn
void swapPointer(char** a, char** b)
{
char* temp = *a;
*a = *b;
*b = temp;
}
char* subBigNumber(char* number1, char* number2)
{
bool sign = false, remember = false;
if (strlen(number1) < strlen(number2))
{
sign = true;
swapPointer(&number1, &number2);
}
else if (strlen(number1) == strlen(number2))
{
for (int i = strlen(number1) - 1; i >= 0; i--)
{
if (number1[i] < number2[i])
{
swapPointer(&number1, &number2);
sign = true;
}
}
}
size_t number1Len = strlen(number1);
size_t number2Len = strlen(number2);
char* result = new char [number1Len + 2];
memset(result, '0', number1Len + 2);
for (int i = 0; i < number2Len; i++)
{
int temp = number1[number1Len - i - 1] - number2[number2Len - i - 1];
if (remember)
temp--;
if (temp < 0)
{
temp += 10;
remember = true;
}
else
remember = false;
result[number1Len - i] = temp + '0';
}
for (int i = 0; i < number1Len - number2Len; i++)
{
int temp = number1[number1Len - number2Len - i - 1] - '0';
if (remember == true)
temp--;
if (temp < 0)
{
temp += 10;
remember = true;
}
else
remember = false;
result[number1Len - number2Len - i] = temp + '0';
}
while (result[0] == '0')
{
if (result[1] != '0' && sign == true)
{
result[0] = '-';
result[number1Len + 1] = '\0';
break;
}
for (int i = 0; i < number1Len; i++)
{
result[i] = result[i + 1];
}
result[number1Len] = '\0';
}
return result;
}