Thuật toán Depth First Search
Thuật toán Depth First Search (DFS – Tìm kiếm theo chiều sâu) là một dạng thuật toán duyệt hoặc tìm kiếm trên cây hoặc đồ thị. Trong lý thuyết khoa học máy tính, thuật toán DFS nằm trong chiến lược tìm kiếm mù (tìm kiếm không có định hướng, không chú ý đến thông tin, giá trị được duyệt) được ứng dụng để duyệt hoặc tìm kiếm trên đồ thị.
Depth First Search (DFS) cùng với Breadth First Search (BFS) là 2 thuật toán cơ bản để chuẩn bị ra các thuật toán phức tạp hơn khi mới tiếp cận Trí tuệ nhân tạo.
Ý tưởng thuật toán
Từ đỉnh (nút) gốc ban đầu.
- Duyệt đi xa nhất theo từng nhánh.
- Khi nhánh đã duyệt hết, lùi về từng đỉnh để tìm và duyệt những nhánh tiếp theo.
- Quá trình duyệt chỉ dừng lại khi tìm thấy đỉnh cần tìm hoặc tất cả đỉnh đều đã được duyệt qua.
Thuật giải
Một số quy ước:
- Open: là tập hợp các đỉnh chờ được xét ở bước tiếp theo theo ngăn xếp (ngăn xếp: dãy các phần tử mà khi thêm phần tử vào sẽ thêm vào đầu dãy, còn khi lấy phần tử ra sẽ lấy ở phần tử đứng đầu dãy).
- Close: là tập hợp các đỉnh đã xét, đã duyệt qua.
- s: là đỉnh xuất phát, đỉnh gốc ban đầu trong quá trình tìm kiếm.
- g: đỉnh đích cần tìm.
- p: đỉnh đang xét, đang duyệt.
Trình bày thuật giải:
- Tập Open chứa đỉnh gốc s chờ được xét.
- Kiểm tra tập Open có rỗng không.
- Nếu tập Open không rỗng, lấy một đỉnh ra khỏi tập Open làm đỉnh đang xét p.
- Nếu p là đỉnh g cần tìm, kết thúc tìm kiếm.
- Nếu tập Open rỗng, tiến đến bước 4.
- Nếu tập Open không rỗng, lấy một đỉnh ra khỏi tập Open làm đỉnh đang xét p.
- Đưa đỉnh p vào tập Close, sau đó xác định các đỉnh kề với đỉnh p vừa xét.
- Nếu các đỉnh kề không thuộc tập Close, đưa chúng vào đầu tập Open. Quay lại bước 2.
- Kết luận không tìm ra đỉnh đích cần tìm.
Code mẫu thuật toán DFS
Hiện thực thuật toán này theo ma trận kề bằng ngôn ngữ C++.
#include <stdio.h>
#include <stack>
using namespace std;
// dinh nghia lop do thi
class Graph
{
private:
int n;
int **edge;
public:
Graph(int size = 2);
~Graph();
bool isConnected(int, int);
void addEdge(int x, int y);
void depthFirstSearch(int, int);
};
Graph::Graph(int size)
{
int i, j;
// xac dinh so dinh cua do thi
n = n < 2 ? 2 : size;
// tao ra cac dinh trong do thi
edge = new int*[n];
for (i = 0; i < n; i++)
edge[i] = new int[n];
// mac dinh giua cac dinh khong co ket noi voi nhau (= 0)
for (i = 0; i < n; i++)
for (j = 0; j < n; j++)
edge[i][j] = 0;
}
Graph::~Graph()
{
for (int i = 0; i < n; ++i)
delete[] edge[i];
delete[] edge;
}
// kiem tra giua hai dinh co ke nhau hay khong
bool Graph::isConnected(int x, int y)
{
return edge[x - 1][y - 1] == 1;
}
// them canh noi dinh x va dinh y
void Graph::addEdge(int x, int y)
{
if (x < 1 || x > n || y < 1 || y > n)
return;
edge[x - 1][y - 1] = edge[y - 1][x - 1] = 1;
}
void Graph::depthFirstSearch(int s, int g)
{
if (s > n || s < 0 || g > n || g < 0)
{
printf("Could not traverse this graph with your request\n");
return;
}
stack<int> open;
bool *close = new bool[n];
int i;
int p;
// mac dinh cac dinh chua duoc duyet
for (i = 0; i < n; i++)
close[i] = false;
// dua dinh goc s vao stack open, chuan bi duyet
open.push(s);
printf("With Depth first Search , we have vertex(s):\n");
while (!open.empty())
{
// lay mot dinh ra khoi open tro thanh dinh dang xet p
do
{
if (open.empty())
return;
p = open.top();
open.pop();
} while (close[p - 1] == true);
// in ra dinh dang xet
printf("%d ", p);
// p da duyet qua
close[p - 1] = true;
// ket thuc duyet khi tim ra ket qua can tim
if (p == g)
return;
// tim dinh ke voi dinh dang xet, dinh nao chua duoc duyet dua vao open
for (i = 1; i <= n; i++)
if (isConnected(p, i) && !close[i - 1])
open.push(i);
}
printf("\n");
delete[] close;
}Ví dụ
Cho đồ thị như hình vẽ
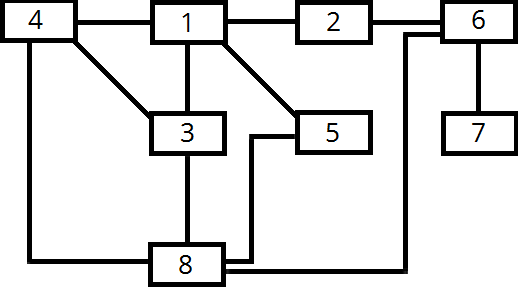
Khởi tạo một đồ thị có 8 đỉnh và có cạnh nối các đỉnh kề như hình vẽ.
void main()
{
// khoi tao do thi
Graph g(8);
// tao canh noi giua cac dinh ke
g.addEdge(1, 2);
g.addEdge(1, 3);
g.addEdge(1, 4);
g.addEdge(1, 5);
g.addEdge(2, 6);
g.addEdge(3, 4);
g.addEdge(3, 8);
g.addEdge(4, 8);
g.addEdge(5, 8);
g.addEdge(6, 7);
g.addEdge(6, 8);
}Chọn đỉnh gốc để duyệt là đỉnh 1 và cần tìm đỉnh 4, thực hiện duyệt ngay sau khi tạo cạnh nối giữa các đỉnh kề.
void main()
{
// khoi tao do thi
Graph g(8);
// tao canh noi giua cac dinh ke
g.addEdge(1, 2);
g.addEdge(1, 3);
g.addEdge(1, 4);
g.addEdge(1, 5);
g.addEdge(2, 6);
g.addEdge(3, 4);
g.addEdge(3, 8);
g.addEdge(4, 8);
g.addEdge(5, 8);
g.addEdge(6, 7);
g.addEdge(6, 8);
// duyet bang Depth First Search
g.depthFirstSearch(1, 4);
}Bảng bên dưới thể hiện quá trình duyệt từ đỉnh 1 đến đỉnh 4.
| Đỉnh đang xét | Các đỉnh kề | Open | Close |
|---|---|---|---|
| {1} | {} | ||
| 1 | {2; 3; 4; 5} | {5; 4; 3; 2} | {1} |
| 5 | {1; 8} | {8; 4; 3; 2} | {1; 5} |
| 8 | {3; 4; 5; 6} | {6; 4; 3; 4; 3; 2} | {1; 5; 8} |
| 6 | {2; 7; 8} | {7; 2; 4; 3; 4; 3; 2} | {1; 5; 8; 6} |
| 7 | {6} | {2; 4; 3; 4; 3; 2} | {1; 5; 8; 6; 7} |
| 2 | {1; 6} | {4; 3; 4; 3; 2} | {1; 5 ;8 ;6; 7; 2} |
| 4 | {1; 3; 8} | {3; 4; 3; 3; 2} | {1; 5; 8; 6; 7; 2; 4} |
Nhận xét
Ưu điểm
- Xét duyệt tất cả các đỉnh để trả về kết quả.
- Nếu số đỉnh là hữu hạn, thuật toán chắc chắn tìm ra kết quả.
Khuyết điểm
- Mang tính chất vét cạn, không nên áp dụng nếu duyệt số đỉnh quá lớn.
- Mang tính chất mù quáng, duyệt tất cả đỉnh, không chú ý đến thông tin trong các đỉnh để duyệt hiệu quả, dẫn đến duyệt qua các đỉnh không cần thiết.
Download mã nguồn
Để tiện lợi, bạn có thể download mã nguồn của giải thuật này tại đây.
