Phép Tích Chập trong Xử Lý Ảnh (Convolution)

Convolution là kỹ thuật quan trọng trong Xử Lý Ảnh, được sử dụng chính yếu trong các phép toán trên ảnh như: đạo hàm ảnh, làm trơn ảnh, trích xuất biên cạnh trong ảnh. Trong bài viết này, tôi trình bày về kỹ thuật tích chập trong lĩnh vực xử lý ảnh và cách hiện thực nó sử dụng ngôn ngữ C++ có hỗ trợ của thư viện openCV.

Định nghĩa

Theo toán học, tích chập là phép toán tuyến tính, cho ra kết quả là một hàm bằng việc tính toán dựa trên hai hàm đã có (f và g).

Ví dụ: đối với phép lọc ảnh, phép tích chập giữa ma trận lọc và ảnh, cho ra kết quả ảnh đã được xoá nhiễu (làm mờ). Tham khảo bài viết Giới Thiệu Ứng Dụng Của Làm Mờ Ảnh (Lọc Nhiễu) Trong Bài Toán Nhận Dạng.

Công thức tích chập giữa hàm ảnh f(x, y) và bộ lọc k(x, y) (kích thước mxn):

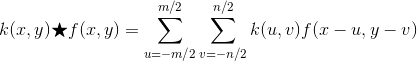
Thành phần không thể thiếu của phép tích chập là ma trận kernel (bộ lọc). Điểm neo (anchor point) của kernel sẽ quyết định vùng ma trận tương ứng trên ảnh để tích chập, thông thường anchor point được chọn là tâm của kernel. Giá trị mỗi phần tử trên kernel được xem như là hệ số tổ hợp với lần lượt từng giá trị độ xám của điểm ảnh trong vùng tương ứng với kernel.

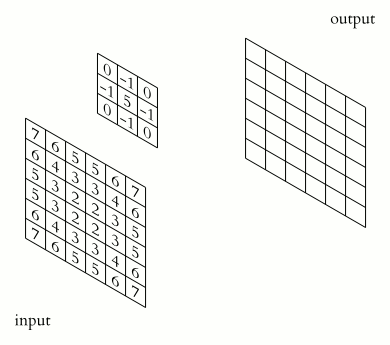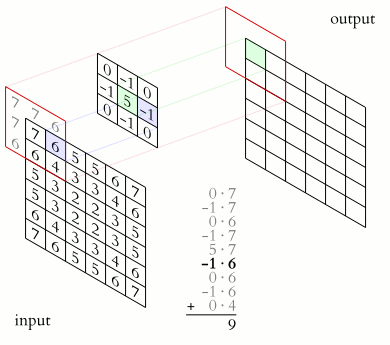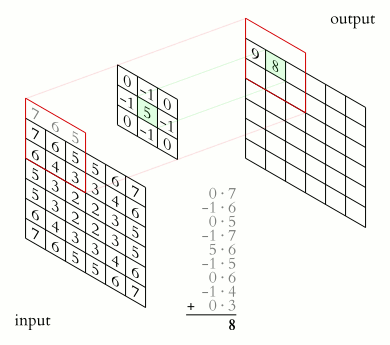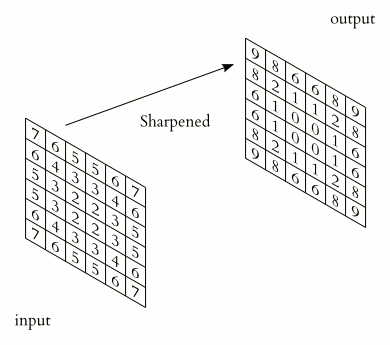
Phép tích chập được hình dung thực hiện bằng việc dịch chuyển ma trận kernel lần lượt qua tất cả các điểm ảnh trong ảnh, bắt đầu từ góc bên trái trên của ảnh. Và đặt anchor point tương ứng tại điểm ảnh đang xét. Ở mỗi lần dịch chuyển, thực hiện tính toán kết quả mới cho điểm ảnh đang xét bằng công thức tích chập.

Xem minh hoạ thực hiện: Ảnh minh hoạ theo thứ tự từ trái qua phải và từ trên xuống dưới. Ảnh cuối cùng là kết quả sau khi thực hiện di chuyển kernel hết toàn bộ ảnh. Ký hiệu: (1) ảnh nguồn, (2) kernel, (3) ảnh kết quả.

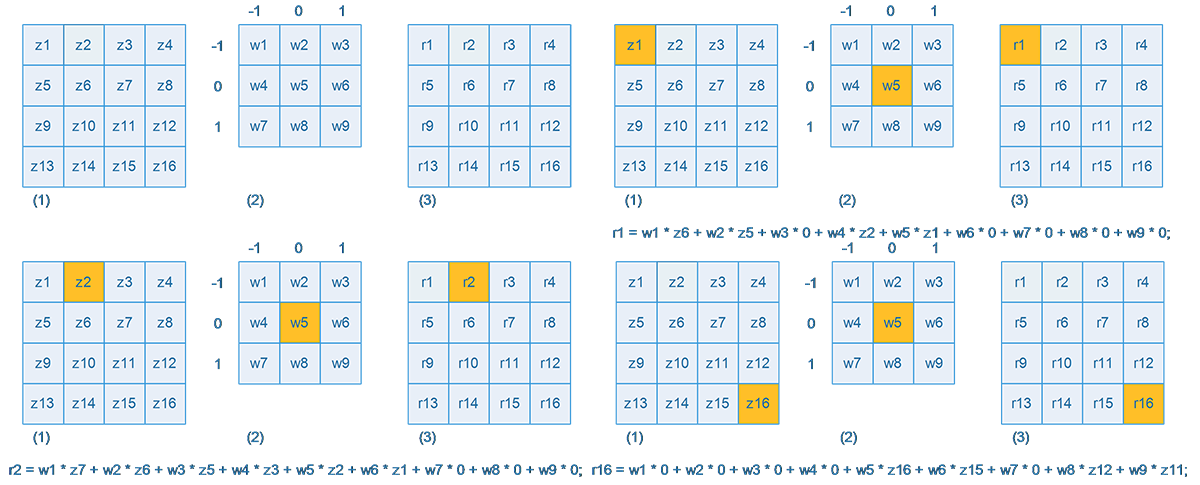
Để dễ hiểu, bạn có thể xoay ma trận kernel góc 180 độ theo chiều kim đồng hồ, sau đó kết quả tích chập chính là tổng các tích của hai phần tử cùng vị trí nằm trên kernel và trên ảnh.

Một số cách xử lý vùng kernel vượt ra ngoài khỏi ảnh:

• Bỏ qua, không thực hiện tính phần tử đó vào kết quả.
• Sử dụng một hằng số để tính toán.
• Duplicate pixel nằm ở biên của ảnh.

Trong bài viết này, tôi sử dụng phương án giải quyết bỏ qua vùng ở ngoài biên, không cho vào kết quả.

Tính chất

Tích chập được định nghĩa là 1 phép toán trên không gian khả tích của các hàm tuyến tính, cho nên nó có tính chất giao hoán, kết hợp và phân phối.

• Giao hoán: f * g = g * f
• Kết hợp: f * g * h = f * (g * h)
• Phân phối: f * g + f * h = f * (g + h)

Do tính chất kết hợp của phép tích chập, khi một phép xử lý ảnh yêu cầu thực hiện tích chập liên tiếp với nhiều bộ lọc (kernel) f * g * h. Ta có thể tính toán trước ma trận kernel để "giảm độ phức tạp tính toán" k = v * h do kích thước ma trận kernel hầu như rất nhỏ so với ảnh. Lúc này, thay vì thực hiện tích chập theo thứ tự r = (f * g) * h, ta thực hiện r = f * (v * h) = f * k.

Ký hiệu:

• - f: hàm ảnh
• - g: bộ lọc thứ nhất
• - h: bộ lọc thứ hai
• - r: hàm ảnh kết quả

Tối ưu thực hiện

Convolution vẫn còn là một kỹ thuật với độ phức tạp tính toán cao. Một số cách dưới đây có thể tối ưu tốc độ của convolution:

• Mỗi phần tử trong ma trận kernel nên là số nguyên: như trong ví dụ trên, các phần tử trong kernel thực ra là số thực, tuy nhiên, tôi thực hiện chuyển sang ma trận số nguyên với số hạng chung cho tất cả các phần tử, kết quả tích chập sẽ nhân cho số hạng chung này.
• Kernel nên thực hiện lưu trong mảng một chiều.
• Tạo ma trận chỉ số truy cập nhanh, với cách này có thể truy cập nhanh đến pixel trên ảnh, tương ứng với kernel mà không cần tính toán chỉ số thêm lần nữa.
  Ví dụ, với kernel (size: 3x3, anchor point: center)

Hiện thực hoá với code

Code chỉ thực hiện với ảnh xám

void Convolution::doConvolution(Mat& sourceImage, Mat& destinationImage)
{
	int nr = sourceImage.rows;
	int nc = sourceImage.cols;

	// Tạo matrix để lưu giá trị pixel sau khi thực hiện tích chập.
	destinationImage.create(Size(nc, nr), CV_8UC1);	

	// Đi lần lượt từng pixel của ảnh nguồn.
	for (int i = 0; i < nr; i ++)
	{
		// Lấy địa chỉ dòng của ảnh đích, để lưu kết quả vào.
		uchar* data = destinationImage.ptr<uchar>(i);	

		for (int j = 0; j < nc; j ++)
		{
			// Lưu tổng giá trị độ xám của vùng ảnh tương ứng với kernel
			int g_val = 0;	

			// Duyệt mask, giá trị pixel đích là tổ hợp tuyến tính của mask với ảnh nguồn.
			for (int ii = 0; ii < _kernel.size(); ii ++)
				{
					// _kernelIndex: mảng chỉ số truy cập nhanh
					int index_r = i - _kernelIndex[ii].x;

					// Với pixel nằm ngoài biên, bỏ qua.
					if (index_r < 0 || index_r > nr - 1)
						continue;

					int index_c = j - _kernelIndex[ii].y;
					if (index_c < 0 || index_c > nc - 1)
						continue;

					g_val += _kernel[ii] * sourceImage.at<uchar>(index_r, index_c);
				}
			
			// Gán giá trị cho matrix đích.
			data[j] = g_val;
		}
	}
}