Thuật Giải A*

08/08/2020•9 min read

Giới thiệu và hướng dẫn hiện thực thuật giải A* - A-star tìm kiếm đường đi tốt nhất trong đồ thị.

Heuristic và hàm Heuristic là gì?

Heuristic là phương pháp giải quyết vấn đề dựa trên phỏng đoán, ước chừng, kinh nghiệm, trực giác để tìm ra giải pháp gần như là tốt nhất và nhanh chóng.

Hàm Heuristic là hàm ứng với mỗi trạng thái hay mỗi sự lựa chọn một giá trị ý nghĩa đối với vấn đề dựa vào giá trị hàm này ta lựa chọn hành động.

A* là gì?

A* là giải thuật tìm kiếm trong đồ thị, tìm đường đi từ một đỉnh hiện tại đến đỉnh đích có sử dụng hàm để ước lượng khoảng cách hay còn gọi là hàm Heuristic.

Từ trạng thái hiện tại A* xây dựng tất cả các đường đi có thể đi dùng hàm ước lược khoảng cách (hàm Heuristic) để đánh giá đường đi tốt nhất có thể đi. Tùy theo mỗi dạng bài khác nhau mà hàm Heuristic sẽ được đánh giá khác nhau. A* luôn tìm được đường đi ngắn nhất nếu tồn tại đường đi như thế.

A* lưu giữ một tập các đường đi qua đồ thị, từ đỉnh bắt đầu đến đỉnh kết thúc, tập các đỉnh có thể đi tiếp được lưu trong tập Open.

Thứ tự ưu tiên cho một đường đi đươc quyết định bởi hàm Heuristic được đánh giá f(x) = g(x) + h(x)

g(x) là chi chi phí của đường đi từ điểm xuất phát cho đến thời điểm hiện tại.
h(x) là hàm ước lượng chi phí từ đỉnh hiện tại đến đỉnh đích f(x) thường có giá trị càng thấp thì độ ưu tiên càng cao.

Thuật giải A*

Open: tập các trạng thái đã được sinh ra nhưng chưa được xét đến.
Close: tập các trạng thái đã được xét đến.
Cost(p, q): là khoảng cách giữa p, q.
g(p): khoảng cách từ trạng thái đầu đến trạng thái hiện tại p.
h(p): giá trị được lượng giá từ trạng thái hiện tại đến trạng thái đích.
f(p) = g(p) + h(p)
- Bước 1:
  - Open: = {s}
  - Close: = {}
- Bước 2: while (Open !={})
  - Chọn trạng thái (đỉnh) tốt nhất p trong Open (xóa p khỏi Open).
  - Nếu p là trạng thái kết thúc thì thoát.
  - Chuyển p qua Close và tạo ra các trạng thái kế tiếp q sau p.
    - Nếu q đã có trong Open
      - Nếu g(q) > g(p) + Cost(p, q)
        
        g(q) = g(p) + Cost(p, q)
        
        f(q) = g(q) + h(q)
        
        prev(q) = p (đỉnh cha của q là p)
    - Nếu q chưa có trong Open
      - g(q) = g(p) + cost(p, q)
      - f(q) = g(q) + h(q)
      - prev(q) = p
      - Thêm q vào Open
    - Nếu q có trong Close
      - Nếu g(q) > g(p) + Cost(p, q)
        
        Bỏ q khỏi Close
        
        Thêm q vào Open
- Bước 3: Không tìm được.

Mô phỏng trên đồ thị

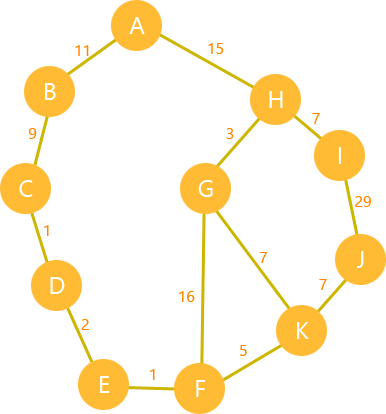
h(A) = 60 / h(B) = 53 / h(C) = 36 / h(D) = 35 / h(E) = 35 / h(F) = 19 / h(G) = 16 / h(H) = 38 / h(I) = 23 / h(J) = 0 / h(K) = 7

Đỉnh bắt đầu A.
Đỉnh kết thúc K.
Ước lượng khoảng cách từ đỉnh hiện tại cho đến đỉnh kết thúc f(x)=g(x)+h(x) trong đó g là khoảng cách ngắn nhất từ đỉnh hiện tại đến đích. Ví dụ: f(A) = 0 + 60.

Bước	P	Các đỉnh nối với P	Open	Close
0			A60
1	A	B, H	B64, H53	A
2	H	G, I, A	B64, G34, I45	A, H
3	G	H, K, F	B64, I45, K32, F53	A, H, G
4	K	G, F, J	B64, J32, F49, I45	A, H, G
5	K (dừng)

Cây tìm kiếm ứng với đồ thị trên.

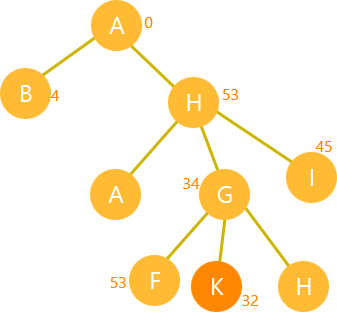
Từ đó mô phỏng thuật toán trên C++ dựa trên đồ thị ở trên.

Hiện thực giải thuật A*

Cách lưu các giá trị trên cây đồ thị

Dùng 2 file Input1.txt và Input2.txt để lưu các trọng số trên cây đồ thị.

File Input1.txt lưu giá trị h của mỗi node mà đề bài cho còn file Input2.txt lưu dưới dạng ma trận lưu khoảng cách giữa 2 điểm nếu giữa 2 điểm không có đoạn nối đánh 0 (tức khoảng cách giữa hai đỉnh này bằng không hoặc không có đoạn nối 2 đỉnh này).

Nội dung file Input1.txt lưu:

11
60 53 36 35 35 19 26 38 23 0 7

Trong đó:

11 là số đỉnh.
Mảng ở dưới là lưu các giá trị h của mỗi đỉnh theo thứ tự.

Nội dung file Input2.txt lưu:

11
0  11  0  0  0  0  0  15 0  0  0 
11 0   9  0  0  0  0  0  0  0  0
0  9   0  1  0  0  0  0  0  0  0
0  0   1  0  2  0  0  0  0  0  0
0  0   0  2  0  11 0  0  0  0  0
0  0   0  0  11 0  16 0  0  0  5
0  0   0  0  0  16 0  3  0  0  7
15 0   0  0  0  0  3  0  7  0  0
0  0   0  0  0  0  0  7  0  29 0
0  0   0  0  0  0  0  0  29 0  7
0  0   0  0  0  5  7  0  0  7  0

Trong đó:

11 là số đỉnh
Ma trận kề ở dưới lưu mỗi liên hệ giữa 2 đỉnh và độ dài 2 đỉnh đó trong đồ thị theo thứ tự của các đỉnh.

Sau đó tạo 1 file main.cpp lưu đoạn code dưới này và chạy chương trình. Chương trình cho kết quả thứ tự các node đi qua từ điểm bắt đầu đến điểm kết thúc.

#include <fstream>
#include <iostream>
using namespace std;

struct Node
{
	int index;  // so thu tu
	int g;      // khoang cach tu dinh ban dau den dinh hien ta
	int f;      // f = h + g;
	int h;      // duong di ngan nhat
	int color;  // danh dau dinh di qua
	int parent;    // dinh cha
};

int a[100][100];
Node p[100];
Node Open[100];
Node Close[100];

void ReadInputFile1(int *b, int &n)
{
	fstream fs1("Input1.txt");

	if (!fs1.is_open())
	{
		cout << "Khong the mo duoc file!";
	}
	else
	{
		fs1 >> n;

		for (int i = 0; i < n; i++)
		{
			fs1 >> b[i];
		}
	}
    fs1.close();
}

void ReadInputFile2(int a[100][100], int &n, int &start, int &finsh)
{
	fstream fs2("Input2.txt");

	if (!fs2.is_open())
	{
		cout << "Khong the mo duoc file!";
	}
	else
	{
		fs2 >> n >> start >> finsh;

		for (int i = 0; i < n; i++)
		{
			for (int j = 0; j < n; j++)
				fs2 >> a[i][j];
		}
	}
	fs2.close();
}

void RhowMatrix(int a[100][100], int n)
{
	for (int i = 0; i < n; i++)
	{
		for (int j = 0; j < n; j++)
		{
			cout << a[i][j] << "\t";
		}
		cout << "\n";
	}
}

int Count(int n, Node *Open)
{
	int count = 0;
	for (int i = 0; i < n; i++)
	{
		if (Open[i].color == 1)
			count++;
	}
	return count;
}

int Find(int n, Node *Open)
{

	for (int i = 0; i < n; i++)
		if (Open[i].color == 1)
			return i;
    return -1;
}

int FindMin(int n, Node *Open)
{
	int minIndex = Find(n, Open);
	int min = Open[minIndex].f;
	for (int i = 0; i < n; i++)
	{
		if (Open[i].f < min && Open[i].color == 1)
		{
			minIndex = i;
			min = Open[i].f;
		}
	}
	return minIndex;
}

void Init(int n, int *b)
{
	for (int i = 0; i < n; i++)
	{
		p[i].index = i;
		p[i].color = 0;
		p[i].g = b[i];
		p[i].parent = 0;
		p[i].f = p[i].g;
		p[i].h = 0;
	}
}

int FindPoint(int n, Node *q, int o)
{
	for (int i = 0; i < n; i++)
		if (q[i].index == o)
			return  i;
    return -1;
}

void AStar(int a[100][100], int n, int start, int finsh, int b[])
{
	int l = 0;
	Open[l] = p[start];
	Open[l].color = 1;
	Open[l].f = Open[l].h + Open[l].g;
	l++;
	int w = 0;

	while (Count(l, Open) != 0) // kiem tra xem tap Open co con phan tu nao khong
	{
		int k = Findmin(n, Open); // tim vi tri nho nhat trong Open
		Open[k].color = 2; // cho diem tim duoc vao Close
		Close[w] = Open[k];
		Close[w].color = 2;
		w++;
		p[FindPoint(n, p, Open[k].index)].color = 2;
		if (FindPoint(n, p, Open[k].index) == finsh)
		{
			cout << "Duong di qua  la" << endl;
			cout << finsh << "\t";
			int y = FindPoint(w, Close, finsh);
			int u = Close[y].parent;
			while (u != start)
			{
				y = FindPoint(w, Close, u);
				u = Close[y].parent;
				cout << u << "\t";
			}
			break;
		}
		else
		{
			for (int i = 0; i < n; i++)
			{
				if (a[FindPoint(n, p, Open[k].index)][i] != 0 && p[i].color == 0) // neu chua co trong Open va Close
				{
					Open[l] = p[i];
					Open[l].color = 1;
					Open[l].h = a[FindPoint(n, p, Open[k].index)][i] + Open[k].h; // tinh h khoang cach ngan nhat tu dinh bat dau den dinh hien tai 
					Open[l].f = Open[l].g + Open[l].h;
					Open[l].parent = FindPoint(n, p, Open[k].index);
					p[i].color = 1;
					l++;
				}
				if (a[FindPoint(n, p, Open[k].index)][i] != 0 && p[i].color == 1) // neu dinh da co trong Open
				{
					int h = FindPoint(l, Open, p[i].index);
					Node tempNode = p[i];
					tempNode.color = 1;
					tempNode.h = a[FindPoint(n, p, Open[k].index)][i] + Open[k].h;
					tempNode.parent = k;
					tempNode.f = tempNode.h + tempNode.g;
					if (tempNode.f < Open[h].f) // neu f trang thai hien tai be hon trang thai cap nhat truoc do			
						Open[h] = tempNode;
				}
				if (a[FindPoint(n, p, Open[k].index)][i] != 0 && p[i].color == 2) // neu dinh da co trong Close
				{
					int h = FindPoint(l, Close, p[i].index);
					Node tempNode = p[i];
					tempNode.color = 1;
					tempNode.h = a[FindPoint(n, p, Open[k].index)][i] + Open[k].h;
					tempNode.parent = k;
					tempNode.f = tempNode.h + tempNode.g;
					if (tempNode.f < Close[h].f) // neu f trang thai hien tai be hon trang thai truoc do	
					{
						Open[l] = tempNode; // them vao Open
						Close[h].color = 1; // danh dau dinh do thuoc Open						
						l++;
					}
				}
			}
		}
	}
}

int main()
{
	int n;	
	int start;
	int finish;
	int b[100];

	ReadInputFile1(b, n);
	ReadInputFile2(a, n, start, finish);

	Init(n, b);
	cout << "Dinh bat dau" << endl;
	cout << start << endl;
	cout << "Dinh ket thuc" << endl;
	cout << finsh << endl;

	AStar(a, n, start, finish, b);
	return 0;
}

Nhận xét

Ưu điểm

Một thuật giải linh động, tổng quát, trong đó hàm chứa cả tìm kiếm chiều sâu, tìm kiếm chiều rộng và những nguyên lý Heuristic khác. Nhanh chóng tìm đến lời giải với sự định hướng của hàm Heuristic. Chính vì thế mà người ta thường nói A* chính là thuật giải tiêu biểu cho Heuristic.

Nhược điểm

A* rất linh động nhưng vẫn gặp một khuyết điểm cơ bản - giống như chiến lược tìm kiếm chiều rộng - đó là tốn khá nhiều bộ nhớ để lưu lại những trạng thái đã đi qua.