Tìm hiểu thuật toán Midpoint
Đường tròn có tâm O(xc, yc) = (0, 0), bán kính r có phương trình:
x2 + y2 = r2 => x2 + y2 - r2 = 0
Đặt f(x, y) = x2 + y2 - r2
Với mọi điểm P(x, y) nằm trong hệ tọa độ Oxy:
- P(x, y) nằm trên đường tròn O nếu f(x, y) = 0
- P(x, y) nằm ngoài đường tròn O nếu f(x, y) > 0
- P(x, y) nằm trong đường tròn O nếu f(x, y) < 0
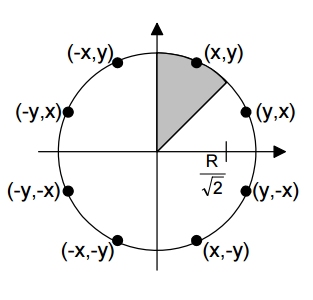
Do đường tròn có tính đối xứng qua các cung 1/8, nghĩa là ứng với một điểm có tọa độ (x, y) thuộc 1 cung bất kỳ, có thể hoàn toàn xác định được tọa độ 7 điểm còn lại bằng cách lấy đối xứng qua các cung.
Từ tính chất đó nên chỉnh cần vẽ 1/8 đường tròn là đủ, sau đó sẽ lấy đối xứng để được đường tròn hoàn chỉnh.
Điểm đầu tiên vẽ là điểm (x = 0, y = R)
Trong cung 1/8 thứ nhất do khoảng biến thiên của x lớn hơn khoảng biến thiên của y, nên xi+1 = xi + 1.
Giả sử đã vẽ được (Xi, Yi) ở bước thứ i, cần xác định (Xi+1, Yi+1) ở bước thứ i + 1.
Xi+1 = Xi+1
Yi+1 ∈ {Yi, Yi - 1}
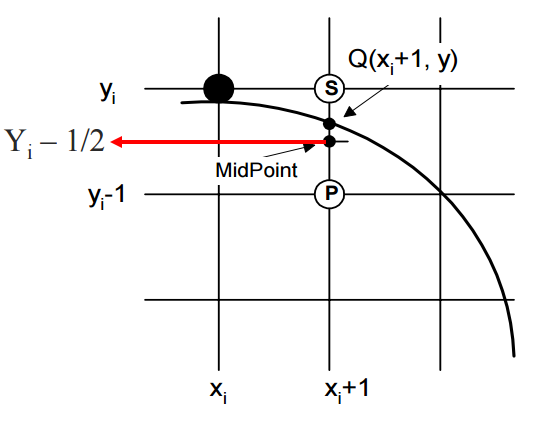
Tính Fi
Đặt Fi = F(X, Y - 1/2):
F(Xi + 1, Yi - 1/2) = (Xi + 1)2 + (Yi - 1/2)2 - R2
Fi = Xi2 + 2Xi + Yi2 - Yi + 5/4 - R2
Nếu Fi < 0 ⇔ (Xi+1, Y) gần với Yi ⇒ Yi+1 = Yi
Nếu Fi ≥ 0 ⇔ (Xi+1, Y) gần với Yi -1 ⇒ Yi+1 = Yi-1
Tính Fi +1 theo Fi
Fi+1 - Fi = 2Xi + 3 + (Yi + 12 - Yi2)+ (Yi+1 - Yi) (*)
Nếu Fi < 0 thì Fi+1 = Fi + 2Xi + 3, do thay thế Yi+1 = Yi vào (*)
Nếu Fi ≥ 0 thì Fi+1 = Fi + 2(Xi - Yi) + 5, do thay thế Yi+1 = Yi-1 vào (*)
Tính giá trị F đầu tiên
F(Xi + 1, Yi - 1/2) = (Xi + 1)2 + (Yi - 1/2)2 - R2
Fi = Xi2 + 2Xi + Yi2 - Yi + 5/4 - R2
Thay Xi = 0 và Yi = R trong công thức trên:
F = 5/4 - R
Hiện thực thuật toán Midpoint
Hàm vẽ 8 điểm đối xứng nhau
void put8pixel(int xc, int yc, int x, int y, int color)
{
putpixel(x + xc, y + yc, color);
putpixel(-x + xc, y + yc, color);
putpixel(x + xc, -y + yc, color);
putpixel(-x + xc, -y + yc, color);
putpixel( y + xc, x + yc, color);
putpixel(-y + xc, x + yc, color);
putpixel(y + xc, -x + yc, color);
putpixel(-y + xc, -x + yc, color);
}
Hàm vẽ đường tròn
void drawCircleMidpoint(int xc, int yc, int r, int color)
{
int x = 0, y = r;
int f = 1 - r;
put8pixel(xc, yc, x, y, color);
while (x < y)
{
if (f < 0) f += (x << 1) + 3;
else
{
y--;
f += ((x - y) << 1) + 5;
}
x++;
put8pixel(xc, yc, x, y, color);
}
}
Chương trình chính
int main()
{
int gd = DETECT, gm;
initgraph(&gd, &gm, "c:\\tc\\bgi");
drawCircleMidpoint(200, 200, 100, colors::BLUE);
Sleep(3000);
closegraph();
return 0;
}