Thuật Toán Vẽ Đường Thẳng Bresenham

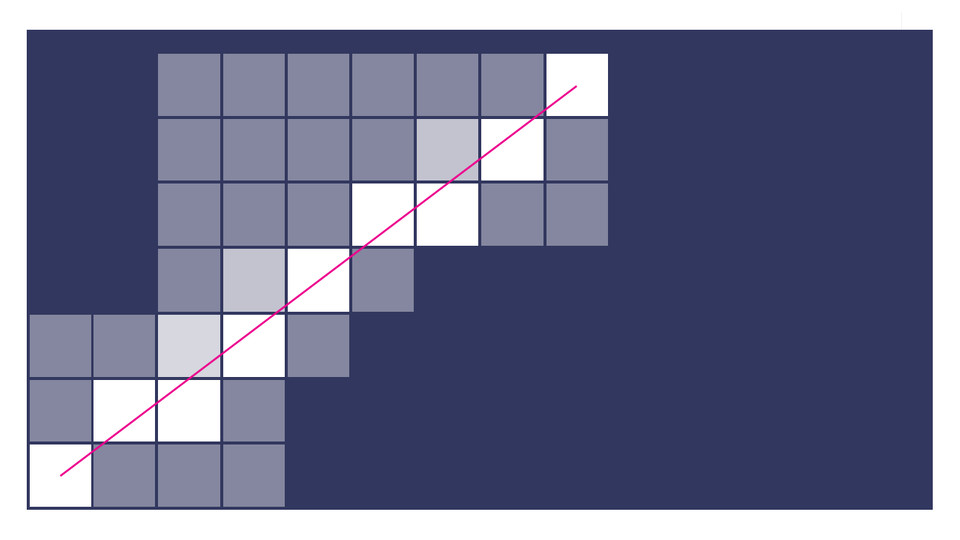
Để vẽ được đường thẳng trên màn hình máy tính cần xác định được điểm ảnh vẽ tiếp theo trên màn hình. Khác với thuật toán Midpoint, thuật toán Bresenham có thể xác định được điểm cần tìm dựa vào khoảng cách giữa đường thẳng thực tế với các điểm nằm trong vùng lựa chọn.

Mô tả thuật toán vẽ đường thẳng Bresenham

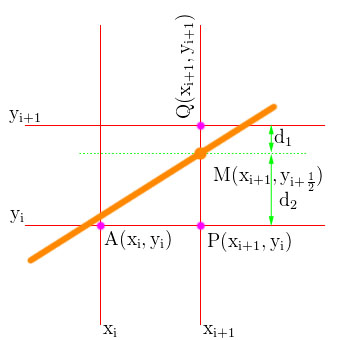
Xét trường hợp: 0 < m < 1

y = m * x + b
m = Δy / Δx

Nhìn vào hình trên có:

d1 = yi + 1 - y = yi + 1 - m * (xi + 1) - b
d2 = y - yi = m * (xi + 1) + b - yi

⇒ d2 - d1
= m * (xi + 1) + b - yi - (yi + 1 - m * (xi + 1) - b)
= 2 * m * (xi + 1) - 2 * yi + 2 * b - 1
= 2 * (Δy / Δx) * (xi + 1) - 2 * yi + 2 * b - 1

⇔ Δx(d2 - d1) = 2 * Δy * xi - 2 * Δx * yi + c = pi, c = -2 * yi + 2 * b - 1 (1)

Mà:

0 < m < 1 ⇒ Δx > 0

Nên dấu của pi phụ thuộc vào d2 – d1.

• Nếu pi < 0 chọn P để vẽ.
• Nếu pi > 0 chọn Q để vẽ.

Mặt khác:

pi+1 = 2 * Δy * xi+1 - 2 * Δx * yi+1 + c
⇒ pi+1 - pi = 2 * Δy * (xi+1 - xi) - 2 * Δx * (yi+1 - yi)
⇒ pi+1 = pi + 2 * Δy * (xi+1 - xi) - 2 * Δx * (yi+1 - yi)

Tìm p_i+1

Trường hợp 1: Chọn P

Khi đó:

xi+1 = xi + 1, xy+1 = yi
⇒ pi+1 = pi + 2 * Δy

Trường hợp 2: Chọn Q

Khi đó:

xi+1 = xi + 1, xy+1 = yi + 1
⇒ pi+1 = pi + 2 * (Δy - Δx)

Tìm p₀

Thay tọa độ (x1, y1) vào (1) được:

p0 = 2 * Δy - Δx

Thuật giải

Input: (x1, y1), (x2, y2)

Output: Tập hợp điểm có tọa độ nguyên.

Các bước thực hiện chính:

Bước 1

dx = x2 - x1, dy = y2 - y1;
d = 2dy - dx;
x = x1, y = y1;
// Vẽ điểm (x,y)

Bước 2

while (x <= x2)
{
    Nếu p > 0 thì:
     	x = x +1;
        y = y;
    	d = d + 2 * dy;
	Nếu p < 0 thì:
        x = x + 1;
        y = y + 1;
    	d = d + 2*(dy – dx);

	// Vẽ điểm (x,y)
}

Hiện thực

void bresenhamLine(int x1, int y1, int x2, int y2)
{
	int Dx = x2 - x1;
	int Dy = y2 - y1;
	int x = x1;
	int y = y1;

	putpixel(x1, y1, BLUE);

	int D = (Dy << 1) - Dx; // ~ int D = 2 * Dy - Dx;

	while(x <= x2)
	{
		x++;
		if (D < 0)
		{
			D = D + (Dy << 1); // ~ D = D + 2*Dy;
		}
		else 
		{
			D = D + ((Dy - Dx) << 1); // D = D + 2*(Dy - Dx);
			y++;
		}
		putpixel(x, y, BLUE);
	}
}