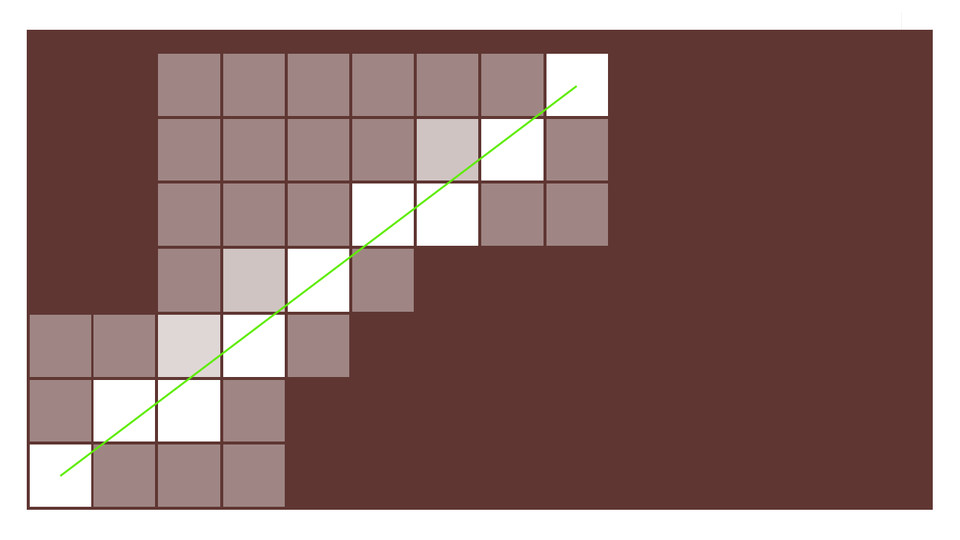
Trong toán học, khái niệm đường thẳng là 1 đường kéo dài vô cùng mỏng, thẳng tuyệt đối; qua hai điểm bất kì chỉ có một đường thẳng đi qua nó.
Trên một màn hình máy tính lại bao gồm nhiều điểm ảnh với các kích thước cụ thể khác nhau. Vì vậy, khái niệm đường thẳng ở đây lại là một tập hợp các điểm có kích thước xấp xỉ gần đúng với các điểm trên thực tế.
Để thu được đường thẳng tốt nhất thì cần lựa chọn được các điểm ảnh gần đúng với đường thẳng thực tế nhất. Do đó, các thuật toán vẽ đường thẳng ra đời nhằm giải quyết bài toán trên.
Để vẽ được đường thẳng nối từ hai điểm (x1, y1), (x2, y2), cần tính toán được điểm vẽ tiếp theo sau khi vẽ điểm đầu tiên (x0, y0).
Với thuật toán Midpoint, có thể tìm được điểm cần tìm dựa vào vị trí trung điểm của các đối tượng đang nằm trong vùng lựa chọn so với đường thẳng đang được vẽ.
Mô tả thuật toán
Đối với việc lựa chọn điểm vẽ tiếp theo sau A, có hai lựa chọn đó là điểm P và Q với M là trung điểm giữa chúng. Việc quyết định chọn điểm nào để vẽ tiếp theo phụ thuộc vào vị trí của M so với đường thẳng đang vẽ. Nếu M nằm phía dưới đường thẳng, chọn điểm Q. Ngược lại, nếu M nằm phía trên đường thẳng ta chọn điểm P.
Xét trường hợp 0 < m < 1
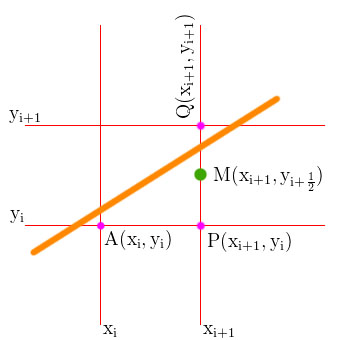
Phương trình đường thẳng là:
y = m * x + b, m = dy / dx
⇔ y = dx / dx * x + b
⇔ dy * x + (-dx * y) + b * dx = 0 (1)
Mà:
F(x, y) = a * x + b * y + c = 0 (2)
(1), (2) ⇒ a = dy, b = -dx, c = b * dx
Tìm d
F(M) = F(xi + 1, yi + 1 / 2)
= F(xi, yi) + a + b / 2 = 0 + dy + dx / 2 = dy + dx / 2
Tìm dmax
Đặt d = F(M)
- Nếu
d > 0, chọn điểmQđể vẽ. - Nếu
d < 0, chọn điểmPđể vẽ.
Trường hợp 1 - chọn Q
Mnew * (xi + 2, yi + 1 / 2) ⇒ dnew = F(xi + 2, yi + 1 / 2)
(Δd)Q = dnew - dold
= F(xi + 1, yi + 1 / 2) - F(xi + 2, yi + 1 / 2) = a
= dy
⇒ dnew = dold + dy
Trường hợp 2 - chọn P
Mnew * (xi + 2, yi + 3 / 2) ⇒ dnew = F(xi + 2, yi + 3 / 2)
(Δd)P = dnew - dold
= F(xi + 1, yi + 1 / 2) - F(xi + 2, yi + 3 / 2) = a + b
= dy - dx
⇒ dnew = dold + dy - dx
Thuật giải
Thuật giải dưới đây chỉ nêu và hiện thực thuật toán trong trường hợp 0 < m < 1, các trường hợp còn lại có thể suy luận tương tự như trên.
Input: (x1, y1), (x2, y2)
Output: Tập hợp điểm có tọa độ nguyên.
Các bước thực hiện chính:
Bước 1
dx = x2 – x1, dy = y2 – y1; d = dy – dx/2; x = x1, y = y1; // Vẽ điểm (x, y)
Bước 2
while (x <= x2)
{
Nếu d > 0 thì:
x = x + 1;
y = y;
d = d + dy;
Nếu d < 0 thì:
x = x + 1;
y = y + 1;
d = d + dy – dx;
// Vẽ điểm (x, y)
}Hiện thực
void midpointLine(int x1, int y1, int x2, int y2)
{
int Dx = x2 - x1;
int Dy = y2 - y1;
int x = x1;
int y = y1;
putpixel(x1, y1, MAGENTA);
float D = Dy - (Dx >> 1); // ~ float D = Dy - Dx/2;
while(x <= x2)
{
x++;
if (D < 0 )
{
D = D + Dy;
}
else
{
D = D + (Dy - Dx);
y++;
}
putpixel(x, y, MAGENTA);
}
}