Giải thuật Minimax là một thuật toán đệ quy lựa chọn bước đi kế tiếp trong một trò chơi có hai người. Xét một trò chơi đối kháng trong đó hai người thay phiên đi nước đi của mình như tic-tac-toe, cờ vua, cờ tướng, cờ caro, cờ vây… Khi chơi bạn có thể khai triển hết không gian trạng thái nhưng khó khăn chủ yếu là bạn phải tính toán được phản ứng và nước đi của đối thủ mình như thế nào? Cách xử lý đơn giản là bạn giả sử đối thủ của bạn cũng sử dụng kiến thức về không gian trạng thái giống bạn. Giải thuật Minimax áp dụng giả thuyết này để tìm kiếm không gian trạng thái của trò chơi.
Giải thuật Minimax
Hai đối thủ trong trò chơi được gọi là MIN và MAX luân phiên thay thế nhau đi. MAX đại diện cho người quyết dành thắng lợi và cố gắng tối đa hóa ưu thế của mình, ngược lại người chơi đại diện cho MIN lại cố gắng giảm điểm số của MAX và cố gắng làm cho điểm số của mình càng âm càng tốt. Giả thiết đưa ra MIN và MAX có kiến thức như nhau về không gian trạng thái trò chơi và cả hai đối thủ đều cố gắng như nhau.
Mỗi Node biểu diễn cho một trạng thái trên cây trò chơi. Node lá là Node chứa trạng thái kết thúc của trò chơi.
Giải thuật Minimax thể hiện bằng cách định trị các Node trên cây trò chơi:
- Node thuộc lớp MAX thì gán cho nó giá trị lớn nhất của con Node đó.
- Node thuộc lớp MIN thì gán cho nó giá trị nhỏ nhất của con Node đó.
Từ các giá trị này người chơi sẽ lựa chọn cho mình nước đi tiếp theo hợp lý nhất.
Các bước thuật giải Minimax
- Nếu như đạt đến giới hạn tìm kiếm (đến tầng dưới cùng của cây tìm kiếm tức là trạng thái kết thúc của trò chơi).
- Tính giá trị của thế cờ hiện tại ứng với người chơi ở đó. Ghi nhớ kết quả.
- Nếu như mức đang xét là của người chơi cực tiểu (nút MIN), áp dụng thủ tục Minimax này cho các con của nó. Ghi nhớ kết quả nhỏ nhất.
- Nếu như mức đang xét là của người chơi cực đại (nút MAX), áp dụng thủ tục Minimax này cho các con của nó. Ghi nhớ kết quả lớn nhất.
Ví dụ mô phỏng giải thuật Minimax cho trò chơi Tic-Tac-toe
- MAX đại diện quân đi O.
- MIN đại diện quân đi X.
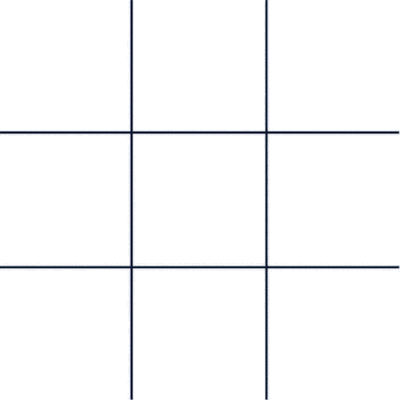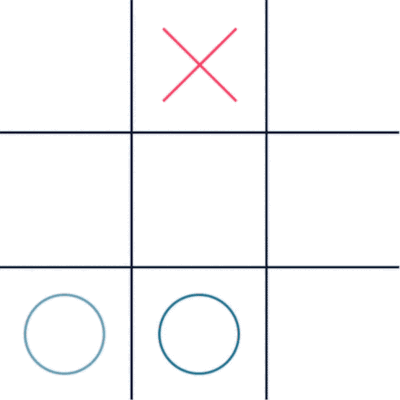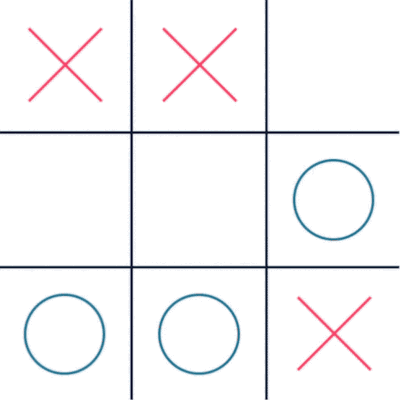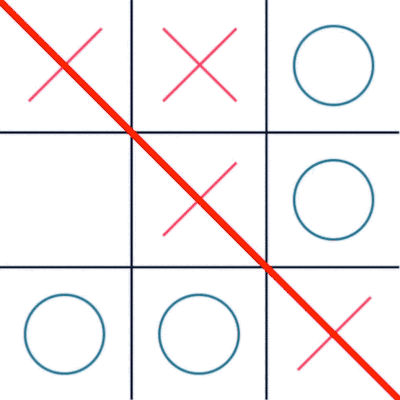
Trạng thái kết thúc là trạng thái có 3 ô liên tiếp ngang, dọc, chéo có cùng một quân cờ X hoặc O, nếu là X tức MIN thắng còn O tức MAX thắng còn nếu tất cả các ô cờ đều được đi và trạng thái chưa kết thúc thì bàn cờ hòa. Điểm thắng của X là -1, của O là 1, và bàn cờ hòa là 0.
Áp dụng giải thuật Minimax:
Từ trạng thái bàn cờ hiện tại ta dự đoán nước đi của trạng thái tiếp theo nếu trạng thái tiếp theo ta tiến hành lượng giá cây trò chơi bằng cách ta tiến hành quét cạn tất cả các trạng thái tiếp theo cho đến lúc gặp trạng thái chiến thắng (Node lá) tính điểm cho Node lá bằng cách:
- Nếu ở trạng thái mà ta gặp chiến thắng nếu đó là lượt đi của quân X thì đánh giá điểm trạng thái đó là -1.
- Nếu ở trạng thái ta gặp chiến thắng nếu đó là lượt đi của quân O thì đánh giá điểm trạng thái đó là 1.
- Nếu là hòa thì điểm trạng thái đó là 0.
Sau đó tính ngược lại cây trò chơi theo quy tắc:
- Nút thuộc lớp MAX thì gán cho nó giá trị lớn nhất của các Node con của Node đó.
- Nút thuộc lớp MAX thì gán cho nó giá trị nhỏ nhất của các Node con của Node đó.
Sau khi lượng giá hết cây trò chơi ta tiến hành chọn bước đi tiếp theo nguyên tắc:
- Nếu lớp tiếp theo là MAX ta chọn Node con có giá trị lớn nhất.
- Nếu lớp tiếp theo là MIN ta chọn Node con có giá trị nhỏ nhất.
Ví dụ
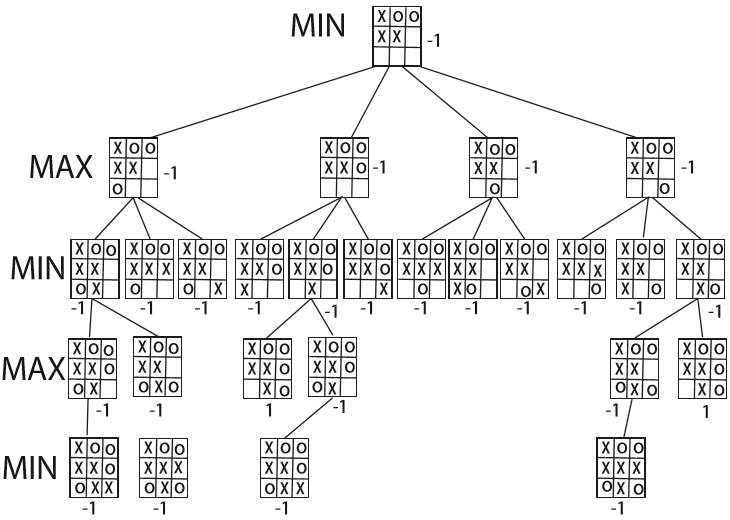
Ưu điểm và khuyết điểm
Ưu điểm
Tìm kiếm được mọi nước đi tiếp theo sau đó lựa chọn nước đi tốt nhất, vì giải thuật có tính chất vét cạn nên không bỏ soát trạng thái.
Khuyết điểm
Đối với các trò chơi có không gian trạng thái lớn như caro, cờ tướng… việc chỉ áp dụng giải thuật Minimax có lẽ không còn hiệu quả nữa do sự bùng nổ tổ hợp quá lớn.
Giải thuật áp dụng nguyên lý vét cạn không tận dụng được thông tin của trạng thái hiện tại để lựa chọn nước đi, vì duyệt hết các trạng thái nên tốn thời gian.
