Đường cong Bézier
Lịch sử hình thành đường cong Bézier
Đường cong Bézier công bố lần đầu vào năm 1962 bởi kỹ sư người Pháp Piere Bézier, sử dụng để thiết kế thân xe ô tô. Thực tế, đường cong Bézier đã được bắt đầu nghiên cứu 3 năm trước đó bởi nhà toán học Paul de Casteljau với giải thuật De Castejiaur để đánh giá các loại đường cong này - theo Wikipedia.
Định nghĩa và các loại đường cong Bézier
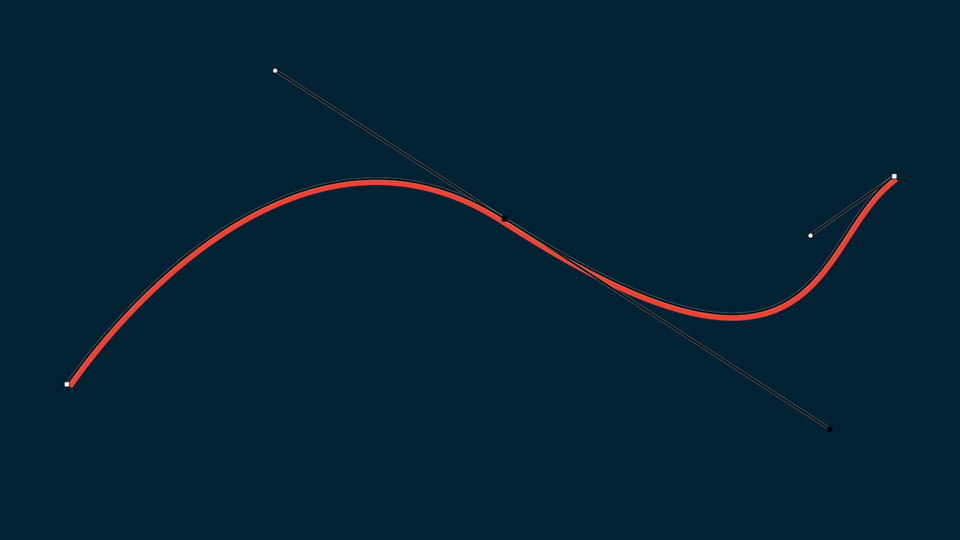
Một đường cong Bézier được xác định bởi tối thiểu hai điểm đầu và cuối (điểm kiểm soát - control point) và tùy theo bậc của nó mà có thêm số lượng các điểm trung gian.
Ví dụ: đường cong Bézier tuyến tính (bậc 1) không có điểm giữa. Đường cong Bézier bậc 2 có tổng cộng 3 điểm, trong đó có một điểm giữa.
Hai điểm đầu và cuối xác định điểm bắt đầu và kết thúc của đường cong. Trong khi đó, các điểm giữa thường không nằm trên đường cong mà chỉ mang tính định hướng cho đường cong.
Đường cong Bézier bậc 1 (tuyến tính)
Phương trình đường cong:
B(t) = P0 + (P1 - P0)t = (1 - t)P0 + tP1, t ∈ [0, 1]
Dễ dàng nhận thấy đường cong Bézier tuyến tính chính là tập hợp đoạn thẳng đi qua 2 điểm P0, P1. Giá trị t tương ứng với khoảng cách từ P0 đến P1.
Ví dụ với t = 0.75:

Đường cong Bézier bậc 2
Đường cong Bézier bậc 2 được tạo thành với 3 điểm P0, P1, P2 cho trước. Có thể tìm phương trình B(t) bằng tập hợp các phương trình sau:
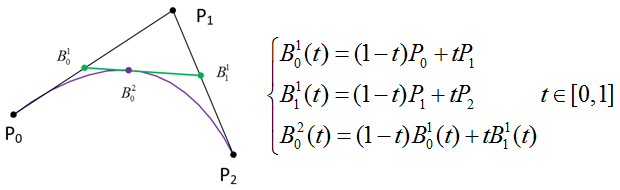
Thế 2 phương trình trên xuống phương trình dưới cùng thu được:
B(t) = (1 - t)2P0 + 2t(1 - t)P1 + t2P2, t ∈ [0, 1]
Đường cong Bézier bậc 3
Một cách tương tự đường cong bậc 2, cũng xây dựng phương trình đường cong như sau:
B(t) = (1 - t)BP0,P1,P2(t) + tBP1,P2,P3(t), t ∈ [0, 1]
Khai triển thu được phương trình đường cong như sau:
B(t) = (1 - t)3P0 + 3t(1 - t)2P1 + 3t2(1 - t)P2 + t3P3, t ∈ [0, 1]
Đường cong Bézier bậc cao (dạng tổng quát)
Sử dụng cách như trên có thể thu được các đường cong bậc 4, bậc 5, ..., bậc n một cách tương tự.
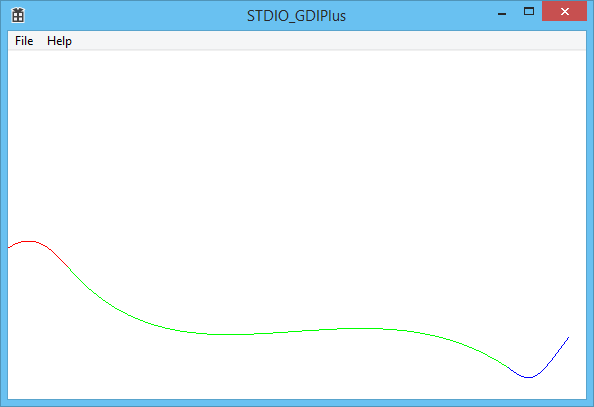
Đường cong Bézier trong GDI+ với C++ Win32 API
Download project mẫu
Khảo sát hàm run() trong file Application.cpp:
void run()
{
if (STDIO_graphic != NULL)
{
/* ---------------------------- DRAW BÉZIER CURVE ---------------------------------*/
Gdiplus::Pen penR(Gdiplus::Color(255, 0, 0));
Gdiplus::Pen penG(Gdiplus::Color(0, 255, 0));
Gdiplus::Pen penB(Gdiplus::Color(0, 0, 255));
auto p11 = normalizeWindowSreen(Gdiplus::PointF(0.0f, SCREEN_HEIGHT*0.75f));
auto p12 = normalizeWindowSreen(Gdiplus::PointF(30.0f, SCREEN_HEIGHT*0.75f + 20));
auto p13 = normalizeWindowSreen(Gdiplus::PointF(50.0f, SCREEN_HEIGHT*0.75f - 10));
auto p14 = normalizeWindowSreen(Gdiplus::PointF(60.0f, SCREEN_HEIGHT*0.75f - 20));
auto p21 = p14;
auto p22 = normalizeWindowSreen(Gdiplus::PointF(180.0f, SCREEN_HEIGHT*0.75f - 160));
auto p23 = normalizeWindowSreen(Gdiplus::PointF(350.0f, SCREEN_HEIGHT*0.75f - 20));
auto p24 = normalizeWindowSreen(Gdiplus::PointF(500.0f, SCREEN_HEIGHT*0.75f - 120));
auto p31 = p24;
auto p32 = normalizeWindowSreen(Gdiplus::PointF(525.0f, SCREEN_HEIGHT*0.75f - 140));
auto p33 = normalizeWindowSreen(Gdiplus::PointF(530.0f, SCREEN_HEIGHT*0.75f - 130));
auto p34 = normalizeWindowSreen(Gdiplus::PointF(560.0f, SCREEN_HEIGHT*0.75f - 90));
STDIO_graphic->DrawBezier(&penR, p11, p12, p13, p14);
STDIO_graphic->DrawBezier(&penG, p21, p22, p23, p24);
STDIO_graphic->DrawBezier(&penB, p31, p32, p33, p34);
/* --------------------------------------------------------------------------------*/
}
}Kết quả